Application

List of packages using OMEinsum

  • GenericTensorNetworks, solving combinational optimization problems by generic tensor networks.
  • TensorInference, probabilistic inference using contraction of tensor networks
  • YaoToEinsum, the tensor network simulation backend for quantum circuits.
  • TensorNetworkAD2, using differential programming tensor networks to solve quantum many-body problems.
  • TensorQEC, tensor networks for quantum error correction.

Example: Solving a 3-coloring problem on the Petersen graph

Let us focus on graphs with vertices with three edges each. A question one might ask is: How many different ways are there to colour the edges of the graph with three different colours such that no vertex has a duplicate colour on its edges?

The counting problem can be transformed into a contraction of rank-3 tensors representing the edges. Consider the tensor s defined as

julia> using OMEinsum
julia> s = map(x->Int(length(unique(x.I)) == 3), CartesianIndices((3,3,3)))3×3×3 Array{Int64, 3}:
[:, :, 1] =
 0  0  0
 0  0  1
 0  1  0

[:, :, 2] =
 0  0  1
 0  0  0
 1  0  0

[:, :, 3] =
 0  1  0
 1  0  0
 0  0  0

Then we can simply contract s tensors to get the number of 3 colourings satisfying the above condition! E.g. for two vertices, we get 6 distinct colourings:

julia> ein"ijk,ijk->"(s,s)[]6

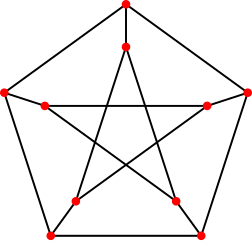
Using that method, it's easy to find that e.g. the peterson graph allows no 3 colouring, since

julia> code = ein"afl,bhn,cjf,dlh,enj,ago,big,cki,dmk,eom->"afl, bhn, cjf, dlh, enj, ago, big, cki, dmk, eom ->
julia> afl, bhn, cjf, dlh, enj, ago, big, cki, dmk, eomERROR: UndefVarError: `afl` not defined in `Main`
Suggestion: check for spelling errors or missing imports.
julia> code(fill(s, 10)...)[]0

The peterson graph consists of 10 vertices and 15 edges and looks like a pentagram embedded in a pentagon as depicted here:

OMEinsum does not optimie the contraction order by default, so the above contraction can be time consuming. To speed up the contraction, we can use optimize_code to optimize the contraction order:

julia> optcode = optimize_code(code, uniformsize(code, 3), TreeSA())SlicedEinsum{Char, DynamicNestedEinsum{Char}}(Char[], afl, laf ->
├─ afl
└─ dlh, dahf -> laf
   ├─ dlh
   └─ dmk, amkhf -> dahf
      ├─ dmk
      └─ agem, kgehf -> amkhf
         ├─ ago, eom -> agem
         │  ├─ ago
         │  └─ eom
         └─ ckbg, ebhcf -> kgehf
            ├─ cki, big -> ckbg
            │  ⋮
            │
            └─ ejbh, cjf -> ebhcf
               ⋮

)
julia> contraction_complexity(optcode, uniformsize(optcode, 3))Time complexity: 2^12.737881076857779
Space complexity: 2^7.92481250360578
Read-write complexity: 2^11.247334178028728
julia> optcode(fill(s, 10)...)[]0

We can see the time complexity of the optimized code is much smaller than the original one. To know more about the contraction order optimization, please check the Julia package OMEinsumContractionOrders.jl.

Confronted with the above result, we can ask whether the peterson graph allows a relaxed variation of 3 colouring, having one vertex that might accept duplicate colours. The answer to that can be found using the gradient w.r.t a vertex:

julia> using Zygote: gradient
julia> gradient(x->optcode(x,s,s,s,s,s,s,s,s,s)[], s)[1] |> sum0.0

This tells us that even if we allow duplicates on one vertex, there are no 3-colourings for the peterson graph.